Month: May 2016

Heap , Hashing , & Tries

Heap
Heap ialah binary tree berstruktur data yg memiliki elemen:
1. Min Heap = Data terkecil dari Heap, Dimana Setiap elemen node lebih kecil daripada children.
2. Max Heap = Data terbesar dari Heap, dimana setiap Elemen Node lebih besar daripada children.

Heap Memiliki 2 metode:
1. Selection’s Algorithm
2. Djikstra’s Algorithm
3. Prim’s Algorithm

 

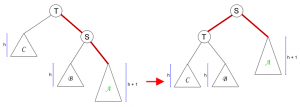
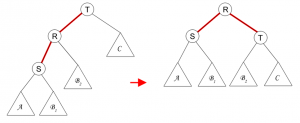
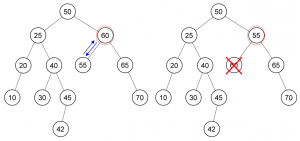
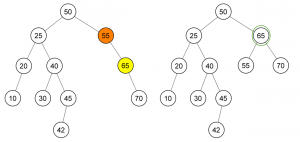
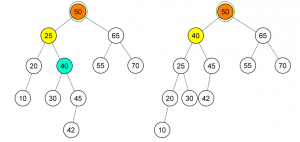
Insertion dalam Min-Max Heap
1. Kalau node parent lebih kecil, tukar uphead max dari parent
2. Kalau node parent lebih besar, tukar dgn uphead min dari parentnya.
3. Upheadmin adalah membandingkan nilai node yang sekarang dengan granparent jika lebih kecil lanjutkan upheadmin node grandparent
4. Upheadmax adalah membandingkan nilai node yang sekarang dengan grand parent dimana jika lebih besar maka di lanjutkan upheadmax node grandparent

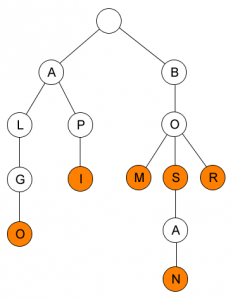
Tries
Tries merupakan struktur data tree yang tersusun digunakan untuk menyetor array.
Contoh:

Hashing
Hashing merupakan transformasi karakter string ke nilai yg lebih pendek. Ada hash table yang berntuh tabel array dimana data asli string tersimpan. Index dari hash tableh dinamakan Hashed key
Contoh:

Beberapa fungsi dari Hash:
1. Mid Square. Mengkotakkan string kemudia gunakan angka bit yg tepat untuk mendapatkan Hash key
2. Division. Membagi string menggunakan operator modulus.
3. Folding. Membagi rata string menjadi bagian bagian untuk mendapatkan hash key.

Red Black BST

Ciri – Ciri:
1. Setiap node memiliki 1 warna
2. Root selalu hitam
3. If node merah, anak selalu hitam

Insertion on Red Black BST
Node Insert selalu merah dan tidak boleh ada 2 merah
Contoh Jika uncle merah

Contoh Jika Uncle Hitam

 

Delete dalam Red Black BST
1. Jika double black node, rotasi sibling red
Ex:
2. Jika double black dan sibling black, ganti jadi merah
Ex:
3. Jika double black sibling black , anak black
Ex:

2-3 Trees
Ciri – Ciri:
1. Setiap node 1 data
2. Kiri < Parent
3. Kanan > Parent
4. Nilai Tengah diantara 2 parent

Insertion
1. Apa bila leaf 2 node maka insert sehingga menjadi 3 node
2. Apa bila leaf 3 node , push middle diantara A dan B hingga split menjadi 2 node, repeat until node sisa 2

Balanced Binary Search Tree
Binary yang balance dalam penataannya agar pengunaan memory lebih sedikit saat pengalokasian

AVL (Adelson-Veleski dan Landis)
Sebuah Metode untuk membalance sebuah BST

Diatas adalah Contoh Balanced

Angka merah lebih dari 1 mendadakan diabukan lah AVL

Cara Merebalance AVL Tree
1. Case LL : T-left-left
2. Case RR : T-right-right
3. Case RL : T-right-left
4. Case LR : T-left-right

LL Rotation Example

RR Rotation Example

RL Rotation Example

 

Deletion on AVL Tree Operation
Example:

 

Keefektifan Data Struktur